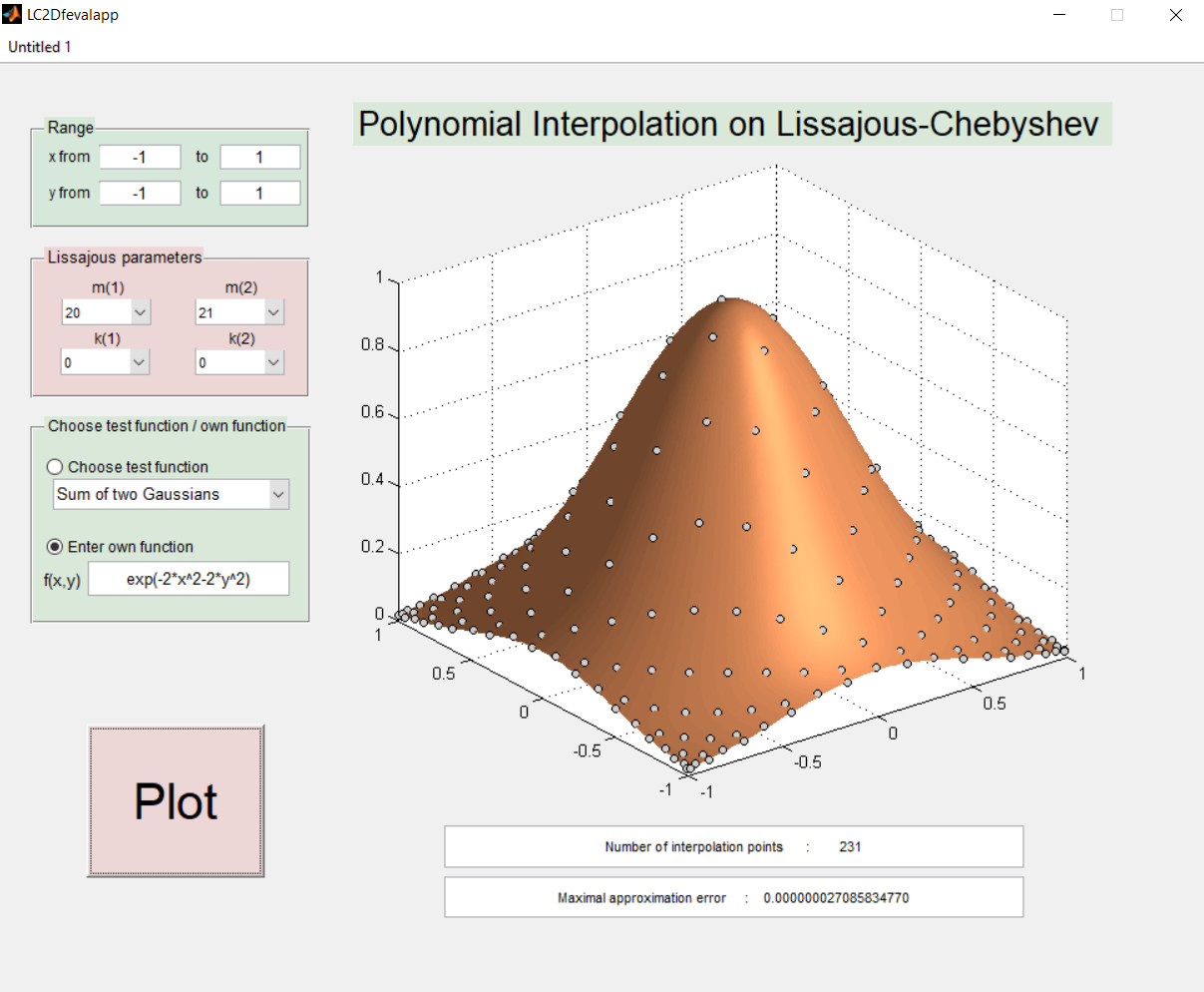
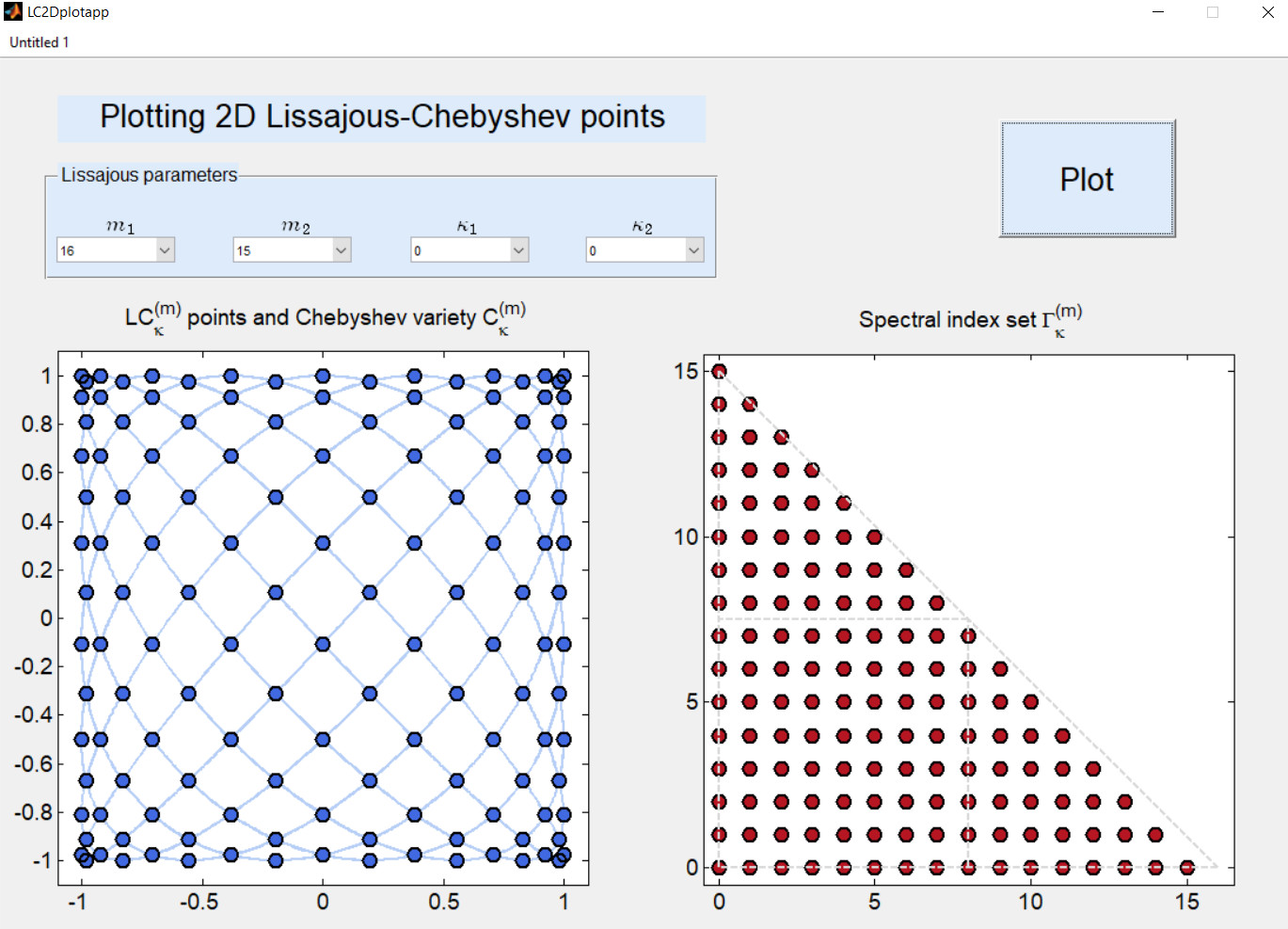
Fig.: Two standalone apps to to test the interpolation schemes and to plot the Lissajous-Chebyshev nodes.


For polynomial interpolation on general Lissajous-Chebyshev points the following packages are available.
  • LC2Ditp: A software package that contains a Matlab implementation for 2D polynomial interpolation on Lissajous-Chebyshev points. Additionally, the two standalone apps LC2Dfevalapp and LC2Dplotapp are included to demonstrate the capabilities of the package.
  • LC3Ditp: A software package that contains a Matlab implementation for 3D polynomial interpolation on Lissajous-Chebyshev points.
For polynomial interpolation along single Lissajous curves, the following software is available
  • LS2Ditp: This software package contains a Matlab implementation for bivariate polynomial interpolation on the node points of degenerate and non-degenerate 2D-Lissajous curves.
  • LD3Ditp: A small software package that contains a Matlab implementation for 3D polynomial interpolation on the node points of degenerate 3D-Lissajous curves.
For spectral interpolation on Lissajous curves in spherical and polar coordinates, the following software tools can be downloaded.
  • LSphere: The package LSphere contains a Matlab-implementation for spectral interpolation on the nodes of spherical Lissajous curves. An application shows how this interpolation tool can be used to estimate the rotation of objects.
  • RDisk: A software package that contains a Matlab implementation to plot rhodonea curves and to calculate spectral interpolants on the unit disk based on rhodonea nodes.
To illustrate some concepts related to signal processing and learning on graphs, the following packages are available.
  • GUPPY: A very simple toolbox to illustrate space-frequency localization and uncertainty principles on graphs.
  • GBFlearn: This package contains Matlab code for kernel-based interpolation, regression and learning on graphs. The involved kernels are generated as generalized shifts of a graph basis function (GBF) and contain geometric information of the graph.
  • GraphWedgelets: This package contains Matlab code for the sparse approximation and compression of images with graph wedgelets. Graph wedgelets are discrete variants of continuous wedgelets and binary space partitionings known from image processing.